Introdução:
Quando se trata de investimentos, entender o risco é fundamental para tomar decisões informadas e bem-sucedidas. Nesse contexto, o desvio padrão e a reta de regressão emergem como ferramentas cruciais para a análise de risco em investimentos. Neste artigo, exploraremos esses conceitos, sua aplicação em investimentos e como podem ajudá-lo a gerenciar melhor o seu portfólio.
Desvio Padrão:
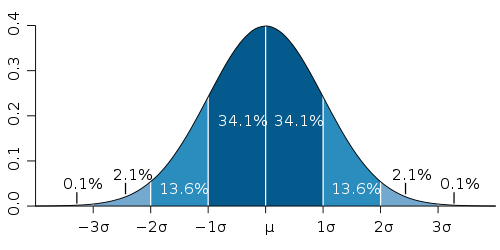
O desvio padrão é uma medida estatística que indica o quão dispersos estão os valores de um conjunto de dados em relação à média desse conjunto. É calculado pela raiz quadrada da variância dos dados e é expresso na mesma unidade que os dados originais. Em investimentos, o desvio padrão é amplamente utilizado para avaliar a volatilidade e o risco de um portfólio. Quanto maior o desvio padrão, maior a volatilidade e, portanto, maior o risco associado ao investimento. Isso ocorre porque um desvio padrão maior indica uma maior dispersão dos retornos em relação à média, o que implica em uma maior incerteza sobre os retornos futuros do investimento.
A fórmula do desvio padrão é dada por:
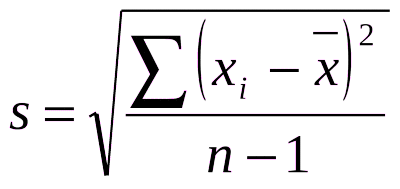
Onde:
- S é o desvio padrão,
- 𝑥𝑖 é cada valor individual do conjunto de dados,
- 𝑥ˉ é a média do conjunto de dados, e
- 𝑁 é o número total de observações.
O desvio padrão nos ajuda a quantificar o risco associado a um investimento e é uma peça fundamental na construção de um portfólio diversificado e balanceado.
Reta de Regressão:
A reta de regressão é uma ferramenta estatística que modela a relação entre duas variáveis. No contexto de investimentos, é frequentemente usada para entender como o desempenho de um portfólio está relacionado a uma variável independente, como os retornos de um índice de mercado.
A regressão linear é calculada pelo método dos Mínimos Quadrados Ordinários (MQO), que consiste em minimizar a soma dos quadrados dos resíduos, ou seja, as diferenças entre os valores observados e os valores previstos pela reta. Isso resulta em uma reta que melhor se ajusta aos dados, minimizando a distância entre os pontos e a reta.
A equação da reta de regressão é dada por:
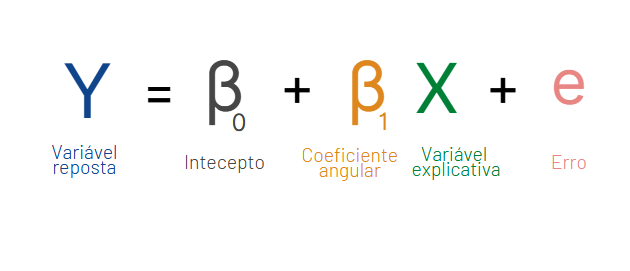
Onde:
- 𝑦 é a variável dependente,
- 𝑥 é a variável independente,
- 𝑏0 é o intercepto da reta, e
- 𝑏1 é o coeficiente angular da reta
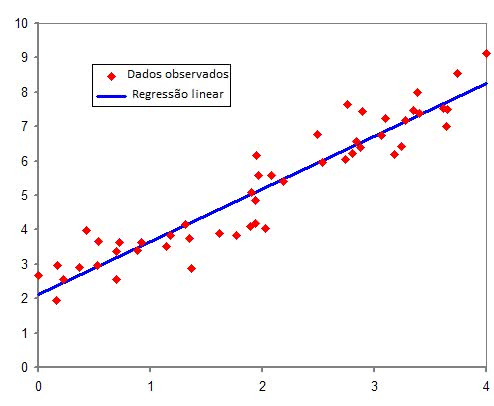
A reta de regressão nos ajuda a entender a relação entre duas variáveis e pode ser útil para prever o desempenho futuro de um investimento com base em uma variável independente.
Conclusão:
O desvio padrão e reta de regressão são ferramentas poderosas na análise de risco em investimentos. Ao entender e aplicar esses conceitos, os investidores podem tomar decisões mais informadas, gerenciar melhor o risco de seus portfólios e buscar retornos mais consistentes ao longo do tempo. É essencial incorporar essas ferramentas em sua análise de investimentos para construir um portfólio robusto e bem-sucedido. Veja abaixo como ela é aplicada dentro do analisador de setups e portfólios da CodeTrading.
As três linhas cinzas que perpassam o gráfico, representam o desvio padrão (linha superior diagonal), desvio padrão negativo (linha inferior diagonal) e reta de regressão (linha central)
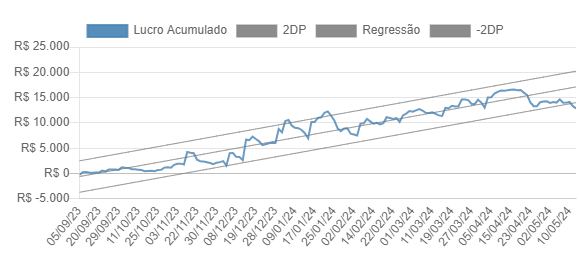
Esperamos que este artigo tenha fornecido uma compreensão mais completa do desvio padrão e reta de regressão, e como essas ferramentas podem ser aplicadas na análise de risco em investimentos. Se você tiver alguma dúvida ou comentário, não hesite em compartilhar conosco. Lembre-se sempre de buscar conhecimento e estar bem informado ao tomar decisões financeiras.
Acesse codetrading.com
Share this content: